Ad quid adhibentur rotae dentatae epicyclicae?

Rotae epicyclicaeEtiam systemata rotarum planetariarum nota, late in variis industriis propter designum compactum, magnam efficientiam, et versatilitatem adhibentur.

Hae dentes imprimis adhibentur in applicationibus ubi spatium limitatum est, sed magnum momentum et variabilitas celeritatis necessariae sunt.

1. Transmissiones Automotivae: Rotae dentatae epicyclicae pars clavis sunt in transmissionibus automaticis, mutationes dentatarum faciles, momentum magnum ad celeritates parvas, et translationem potentiae efficientem praebentes.
2. Machinae Industriales: In machinis gravibus adhibentur propter facultatem onera magna ferendi, momentum torquens aequaliter distribuendi, et in spatiis compactis efficaciter operandi.
3. Aerospatialis: Hae rotae dentatae munus cruciale in motoribus aeroplanorum et rotoribus helicopterorum agunt, firmitatem et accuratam gubernationem motus sub condicionibus difficilibus praestantes.
4. Robotica et Automatio: In robotica, dentes epicyclici adhibentur ad motus accuratum moderandum, designum compactum, et momentum magnum in spatiis angustis assequendum.

Quae sunt quattuor elementa rotarum epicyclicarum?

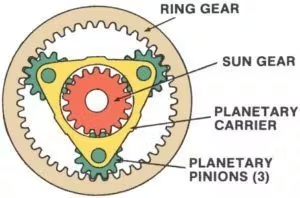
Series rotarum epicyclicarum, etiam nota utrota planetaria Systema, mechanismus valde efficax et compactus est, vulgo in transmissionibus autocineticis, robotica, et machinis industrialibus adhibitus. Hoc systema quattuor elementis praecipuis constat:

1. Apparatus SolisIn centro dentatae posita, dentata solaris est impulsor vel receptor motus primarius. Directe cum dentibus planetariis coniungitur et saepe ut ingressus vel exitus systematis fungitur.

2. Rotae PlanetariaeHae sunt plures rotae dentatae quae circum rotam solarem rotant. In portatore planetario impositae, cum rota et rota solari et rota anulari congruunt. Rotae planetariae onus aequaliter distribuunt, ita ut systema magnum momentum rotatorium sustinere possit.

3.Vector PlanetaeHaec pars rotas planetarias in loco tenet et rotationem eorum circa rotam solarem sustinet. Ferculum planetarium, pro configuratione systematis, tamquam elementum ingressus, egressus, vel stationarium fungi potest.

4.Annulus RotariusHaec est magna rota exterior quae planetas circumdat. Dentes interiores anuli dentati cum planetas congruunt. Sicut alia elementa, anulus dentatus potest fungi ut ingressus, egressus, vel immotus manere.

Interactio horum quattuor elementorum flexibilitatem praebet ad varias rationes celeritatis et mutationes directionum intra structuram compactam consequendas.

Quomodo Rationem Dentaturae in Rota Epicyclica Computare?

Proportio transmissionisapparatus rotarum epicyclicarum Pendet a componentibus fixis, inputibus, et outputibus. Hic est dux gradatim ad rationem transmissionis computandam:

1. Configurationem Systematis Intellege:

Identifica quod elementum (sol, planetae vector, an anulus) immotum sit.

Partes input et output determina.

2. Aequatione Fundamentali Rationis Transmissionis Utere: Ratio transmissionis systematis transmissionis epicyclici calculari potest utens:

GR = 1 + (R / S)

Ubi:

GR = Ratio Transmissionis

R = Numerus dentium in anulo dentato

S = Numerus dentium in rota solari

Haec aequatio valet cum vector planetarius est egressus, et vel sol vel anulus dentatus immobilis est.

3. Aliis Configurationibus Adapta:

• Si rota solaris immota est, celeritas producta systematis afficitur ratione inter rotam anularem et portatorem planetarium.
• Si anulus dentatus immotus est, celeritas producta a relatione inter anulum dentatum et planetam portantem determinatur.

4. Ratio Inversae Transmissionis pro Emissione ad Ingressum: Cum reductionem celeritatis calculas (ingressum maius quam emissionem), ratio simplex est. Pro multiplicatione celeritatis (emissionem maius quam ingressum), rationem calculatam inverte.

Exemplum Computationis:

Ponamus apparatum rotarum habere:

Anulus dentatus (R): dentes 72

Dentes Solis (S): 24 dentes

Si vector planetarius est emissio et rota solaris immota est, proportio transmissionis est:

GR = 1 + (72/24) GR = 1 + 3 = 4

Hoc significat celeritatem productam quater tardiorem fore quam celeritatem ingressam, rationem reductionis 4:1 praebens.

Horum principiorum intellectus ingeniariis permittit ut systemata efficacia et versatilia ad usus specificos accommodata designent.